如何更好地理解KMP算法(C+Python)

摘要：本文通过讲解next数组的生成以及如何使用next数组来实现KMP算法，采取C和Python进行编写。

正文：

关于KMP主要难点是next[]数组，模式串的下一个匹配位k及模式串向右移动的距离m,以下我分三步并结合例子讲解三个难点。

明确概念

• ”前缀”和”后缀”：“前缀”指除了最后一个字符以外，一个字符串的全部头部组合；”后缀”指除了第一个字符以外，一个字符串的全部尾部组合。例如”ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D].
• 最大公共前后缀：基于前缀，和后缀概念，在一个字符串中，最长的相同的前缀和后缀称为最长公共前后缀，有的称之为最长首尾串。
• Next[]数组：Next数组主要用来存放最大公共前后缀的长度值，此值定义为K值，即Next[]数组存储一组k值

举例：

字符串”A”的前缀和后缀都为空，共有元素的长度为0；
字符串”AB”的前缀为[A]，后缀为[B]，无共有元素，长度为0；
字符串”ABA”的前缀为[A, AB]，后缀为[BA, A]，共有元素”A”,长度1；
字符串”ABAB”的前缀为[A, AB, ABA]，后缀为[BAB, AB, B]，共有元素”AB”,长度为2；
字符串”ABABA”的前缀为[A, AB, ABA, ABAB]，后缀为[BABA, ABA, BA, A]，共有元素为”ABA”，长度为3；
字符串”ABABAA”的前缀为[A, AB, ABA, ABAB, ABABA]，后缀为[BABAA, ABAA, BAA, AA, A]，共有元素为”A”，长度为1；
综合以上，由字符串”A”、“AB”、“ABA”、“ABAB”、“ABABA”、“ABABAA”六个字符串组成的Next[]数组的值为：“001231”
即Next[]={0,0,1,2,3,1}

开始匹配

主串S和模式串T进行匹配时的起始位置：均为0

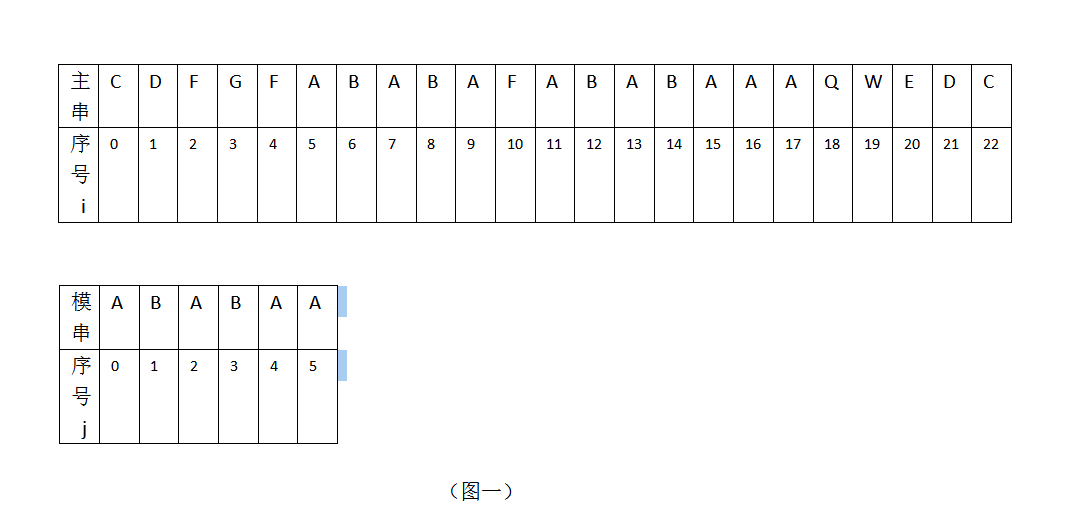
• 模式串下一匹配位：定义为k，即下一次匹配时，主串i不变，模式串的新j值为j=k,即S[i]与T[k]进行比较。
• K如何取值：k=next[j-1]，为何用next[j-1]标识，之所以这样是为了更好的理解，j-1的含义是当j=5，i=10，T[5]!=S[10]时，需要取模式串”ABABAA”的next[]数组的第j-1=4位的数组值，此时Next[]={0,0,1,2,3,1}”，在此next[]数组中，next[4]=3，即k=3。
• 注:还可以用另一个方法计算k，模式串j前面（不包括j），即从位置0开始，到4(j-1=4)结束的字符串”ABABA”的最长公共前后缀为”ABA”，它的长度值为3，即k=3，如下图：

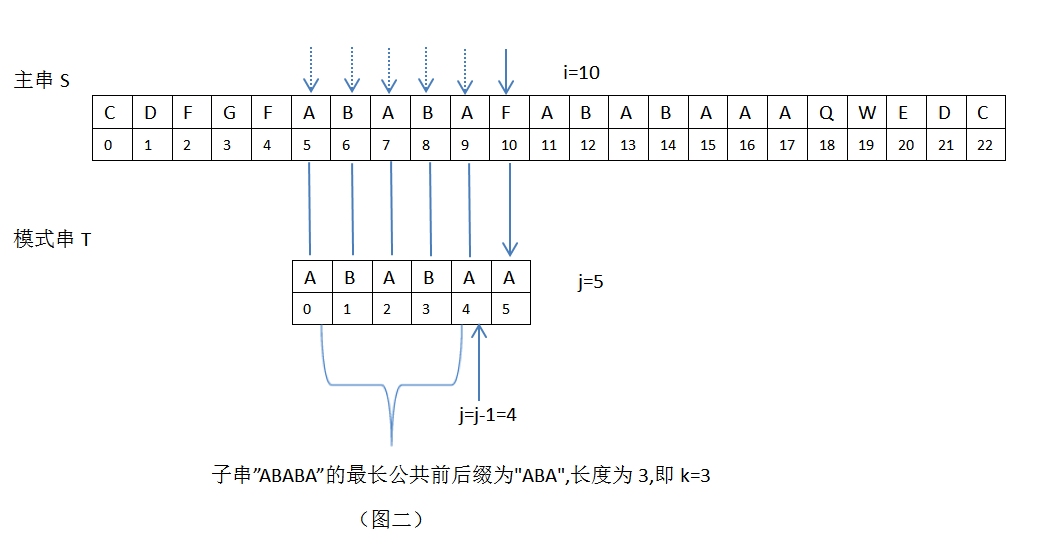
• 模式串T向右滑动的最大距离：定义为m，m=j-k（当j>0时，j为模式串的序号）

• 字符串模式匹配时存在的两种情况：

  1.当模式串j=0时，即T[0]与主串Si且T[0]!=S[i]时，主串S位置加1，T向右滑动1位，此时j=0，T[0]将与主串Si继续比较。

  2.当模式串j>0时，即T[j]与主串Si且T[j]!=S[i]时，此时会用到KMP算法。

举例KMP算法

1.初始时，i =0，j=0；S[0]=”C”，T[0]=”A”，S[i]!=T[j]，匹配失败，此时需要主串S位置加1，模式串T向右移动1位。

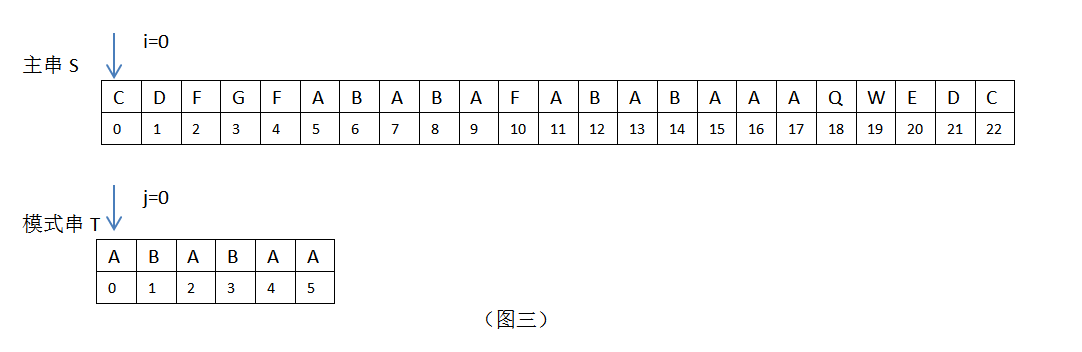
2.当 i =1,2,3,4时，均匹配失败；此时需要主串S位置加1，模式串T向右移动1位。

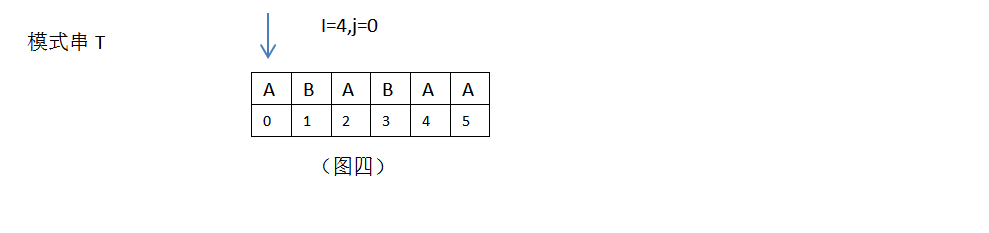
3.当i=5,6,7,8,9，j=0,1,2,3,4时，匹配成功，此时主串S位置加1，模式串T位置加1位。

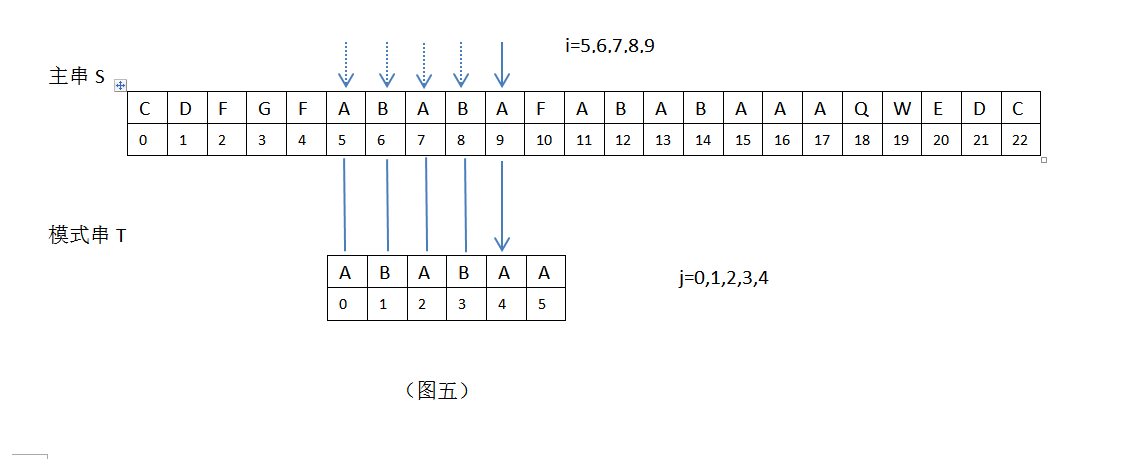
4.当i=10，j=5时，匹配失败，S[10]=“F”， T[5]=“A”，S[10]!=T[5]，见下：

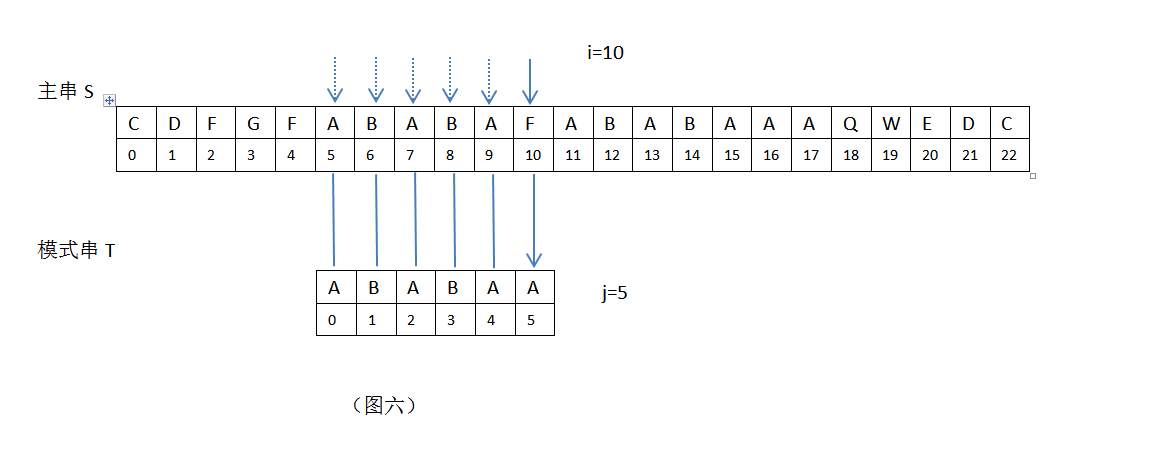
5.在上图，i=10，j=5，接下来继续匹配时，需要主串中S[i]位置不变（i=10），模式串位置变为T[k]，现在需要求k值。根据公式k=next[j-1]，需要取模式串”ABABAA”的next[]数组的第j-1=5-1=4位的数组值，此时Next[]={0,0,1,2,3,1}”，在此next[]数组中，next[4]=3，即k=3（j前面字符串”ABABA”的最长公共前后缀为”ABA”，它的长度值为3，即k=3）；此时，根据KMP算法，i=10不变，模式串T向右滑动m=j-k=5-3=2位，模式串新的j值为j=k=3，见下：

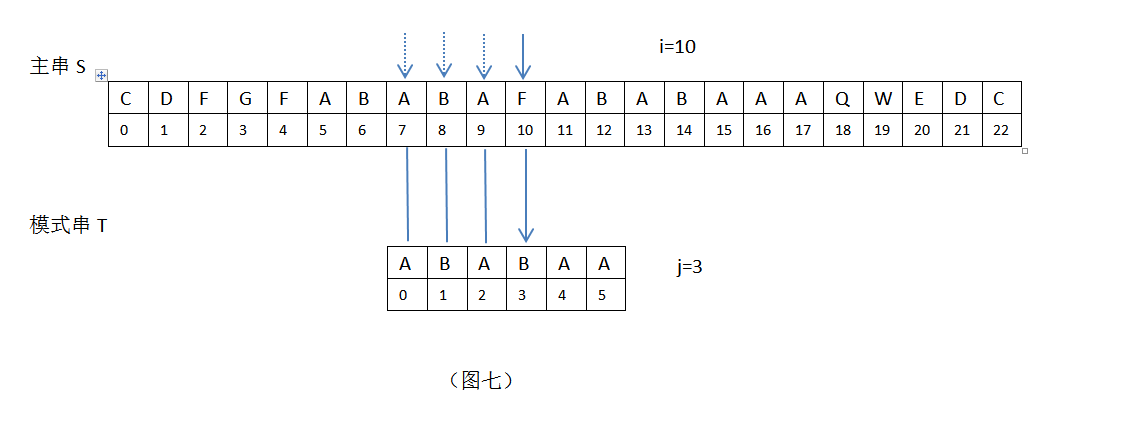
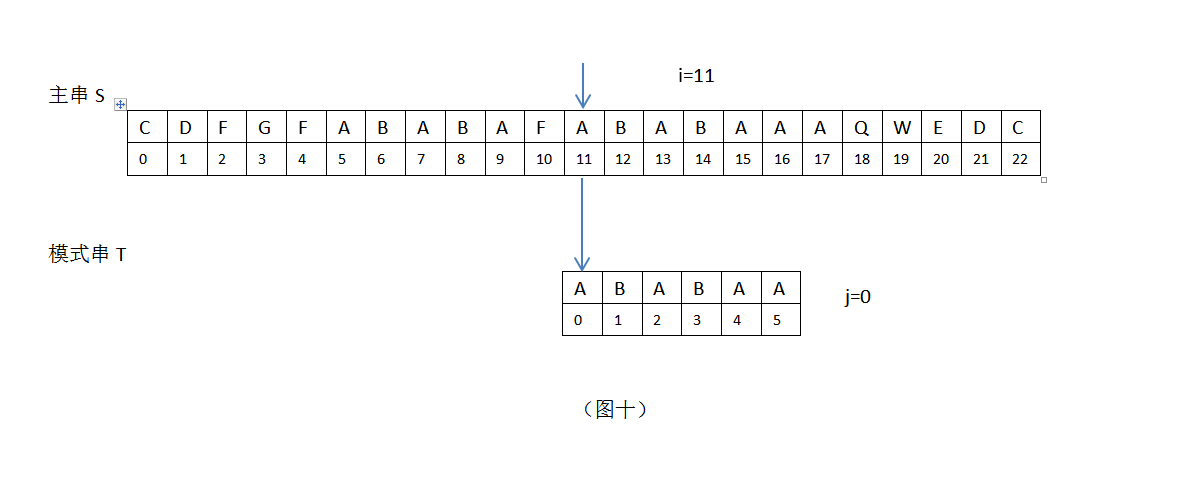
6.在上图，i=10，j=3，S[i]=S[10]=”F” ，T[j]=T[3]=”B”，S[10]!=T[3]，接下来继续匹配时，需要主串中S[i]位置不变（i=10），模式串位置变为T[k]，现在需要求k值。根据公式k=next[j-1]，需要取模式串”ABABAA”的next[]数组的第j-1=3-1=2位的数组值，此时Next[]={0,0,1,2,3,1}”，在此next[]数组中，next[2]=1，即k=1（j前面字符串”ABA”的最长公共前后缀为”A”，它的长度值为1，即k=1）；此时，根据KMP算法，i=10不变，模式串T向右滑动m=j-k=3-1=2位，模式串新的j值为j=k=1，见下：

依此类推：接下来，当i=12,13,14,15,16，j=1,2,3,4,5，匹配成功，模式串T在主串中的位置为11。

C语言版代码

#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int length(char *str)	//这个函数是用来计算字符串的长度
{
    int cnt = 0;
    for(int i = 0;str[i]!='\0';++i)
        ++cnt;
    return cnt;
}

int *KMPnext(char *str)	//定义kmp算法的next数组生成函数
{
    int len = length(str);
    int *next = (int*)malloc(sizeof(int)*len);
    memset(next,0,sizeof(next));
    for(int j=1,k=0;j < len;++j)
    {
        while(k > 0 && str[j] != str[k])
            k = next[k-1];
        if(str[k] == str[j])
            ++k;
        next[j] = k;
    }
    return next;
}

int KMP(char *s,char *t,int *next)
{
    //s为主串，t为模式串
    int s_len = length(s);
    int t_len = length(t);
    for(int i = 0,j = 0; i <s_len;++i)
    {
        while(j > 0 && s[i] != t[j])
            j = next[j-1];
        if(s[i] == t[j])
            ++j;
        if(j==t_len)
            return i-j+1;
    }
    return -1;
}

int main()
{
    char s[30] = "CDFGFABABAFABABAAAQWEDC";
    char t[10] = "ABABAA";
    int local;
    int *next;
    next = KMPnext(t);  //将模式串传入函数求得next数组
    local = KMP(s,t,next);
    printf("%d\n",length(s));
    printf("next数组：");
    for(int i = 0;i<length(t);++i)
        printf(" %d",next[i]);
    printf("\n匹配的位置是：%d",local);
    return 0;
}

Python版代码

#python版KMP算法

def KMP_next(str: str)->[int]:          #定义next数组
    next = [0] * len(str)
    k = 0
    for j in range(1,len(str)):
        while k > 0 and str[j] != str[k]:
            k = next[k-1]
        if str[j] == str[k]:
            k+=1
        next[j] = k
    return next


def KMP(s : str, t : str,next : [int]) -> int:
    #s为主串,t为模式串,next为数组
    j = 0
    for i in range(0,len(s)):
        while j > 0 and s[i] != t[j]:
            j = next[j -1]
        if s[i] == t[j]:
            j = j+ 1
        if j == len(t):
            return i-j+1
    return -1

if __name__ == "__main__":

    s = "CDFGFABABAFABABAAAQWEDC"
    t = "ABABADA"
    next = KMP_next(t)
    print('NEXT数组：',next)
    ans = KMP(s,t,next)
    if ans != -1:
        print('匹配到模式串的位置为：',ans) 
    else:
        print('未匹配到模式串')